martes, 26 de mayo de 2020
jueves, 14 de mayo de 2020
Clasificación de fracciones
Fracciones propias
Se llaman fracciones propias a aquellas que representan números menores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número menor que la unidad se caracterizan por tener el numerador menor que el denominador. Por ejemplo:


Fracciones impropias
Se llaman fracciones impropias a las que representan números mayores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número mayor que la unidad se caracterizan por tener el numerador mayor que el denominador. Por ejemplo:


Fracciones iguales a la unidad
Son las que representan números iguales a la unidad. Es decir, son las fracciones que representan el 1 y se caracterizan por tener el numerador y el denominador iguales.
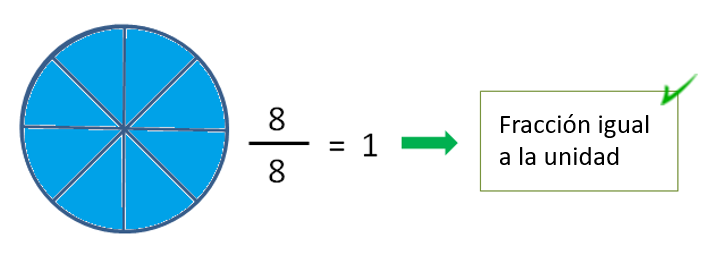
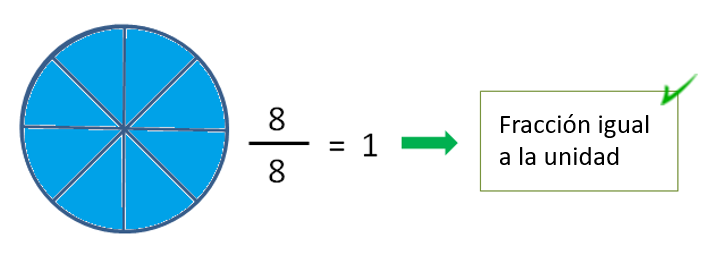
Ejemplos de clasificación de fracciones
Vamos a ver ejemplos clasificando estas fracciones:
2527 ; 12 ; 54 ; 180180 ; 363 ; 66 ; 42 ; 1010 ; 200279
2527 < 1 ya que el numerador es menor que el denominador: Es una fracción propia
12 < 1 ya que el numerador es menor que el denominador: Es una fracción propia
54 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia
180180 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad
363 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia
66 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad
42 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia
1010 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad
200279 < 1 ya que el numerador es menor que el denominador: Es una fracción propia
Fracciones homogéneas y fracciones heterogéneas
Para empezar, vamos a recordar los términos que componen toda fracción.
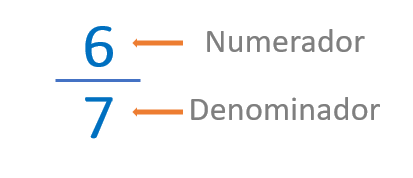
El termino que indica el número de partes en las que dividimos la unidad se llama DENOMINADOR.
El termino que indica el número de partes a las que nos referimos se llama NUMERADOR.
Una vez hemos recordado esto, vamos a ver la relevancia que tienen el denominador para comprender el concepto de fracciones homogéneas o heterogéneas.
Lo primero, es decir que se trata de un concepto que define un tipo de relación que existe entre dos o más fracciones y que depende del denominador que tienen dichas fracciones. De esta forma diremos que:

El termino que indica el número de partes en las que dividimos la unidad se llama DENOMINADOR.
El termino que indica el número de partes a las que nos referimos se llama NUMERADOR.
Una vez hemos recordado esto, vamos a ver la relevancia que tienen el denominador para comprender el concepto de fracciones homogéneas o heterogéneas.
Lo primero, es decir que se trata de un concepto que define un tipo de relación que existe entre dos o más fracciones y que depende del denominador que tienen dichas fracciones. De esta forma diremos que:
Dos fracciones son homogéneas cuando sus denominadores son iguales. Y ¿qué significa esto?
Que dos fracciones sean homogéneas significa que en ambas fracciones el denominador es el mismo, es decir, la unidad está dividida en la misma cantidad de partes y por ello sus denominadores son iguales.
Por ejemplo:
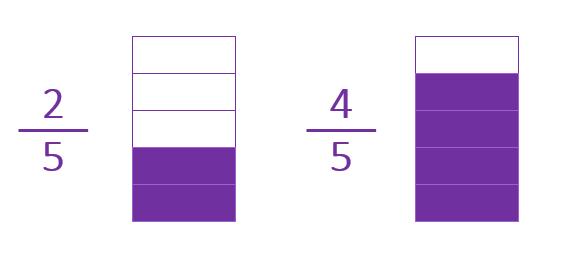
Estas dos fracciones son diferentes, pero su denominador es el mismo.
Por tanto 2/5 y 4/5 son fracciones homogéneas.
Por ejemplo:

Estas dos fracciones son diferentes, pero su denominador es el mismo.
Por tanto 2/5 y 4/5 son fracciones homogéneas.
Dos fracciones son heterogéneas cuando sus denominadores son diferentes. Y, ¿qué significa esto?
Que dos fracciones sean heterogéneas significa que en ambas fracciones la unidad está dividida en una cantidad diferentes de partes y, por eso, sus denominadores son distintos.
Por ejemplo:
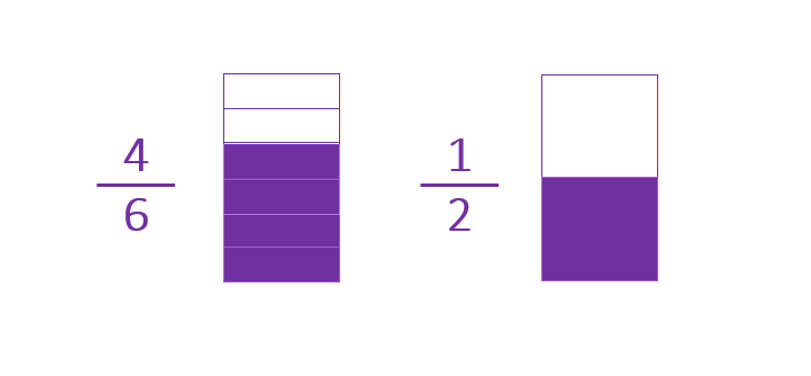
Estás dos fracciones son diferentes y sus denominadores también son diferentes.
Por tanto 4/6 y 1/2 son fracciones heterogéneas.
En principio podría parecer que esto no es un dato relevante pero, al hacer cálculos entre fracciones, el hecho de que los denominadores sean o no iguales puede dificultar nuestra labor.
Por ejemplo:

Estás dos fracciones son diferentes y sus denominadores también son diferentes.
Por tanto 4/6 y 1/2 son fracciones heterogéneas.
En principio podría parecer que esto no es un dato relevante pero, al hacer cálculos entre fracciones, el hecho de que los denominadores sean o no iguales puede dificultar nuestra labor.
Fracciones equivalentes
Fíjate en la siguiente imagen:
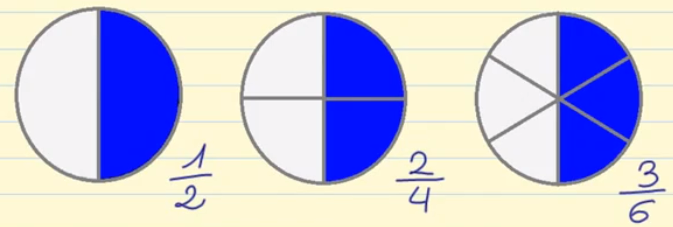 La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes.
Es decir, las tres fracciones dan el mismo resultado, son equivalentes.

La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes.
Es decir, las tres fracciones dan el mismo resultado, son equivalentes.
¿Qué son las fracciones equivalentes?
Son aquellas fracciones que representan la misma cantidad.
¿Cómo sabemos si dos fracciones son equivalentes?
Lo son si los productos del numerador de una y el denominador de la otra son iguales, es decir, productos cruzados.
Vamos a ver unos ejemplos:
Comprobemos si 2/5 y 4/10 son equivalentes.
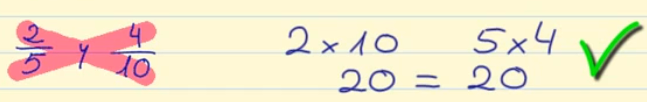 Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.
Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.
2 x 10 = 20 5 x 4 = 20
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.
Ahora vamos a comprobar si 3/7 y 7/3 son fracciones equivalentes.
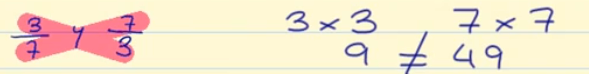 Para ello multiplicamos, como muestra la imagen:
Para ello multiplicamos, como muestra la imagen:
3 x 3 = 9 7 x 7 = 49
Como el resultado no es el mismo, podemos decir que 3/7 y 7/3 no son equivalentes.
Vamos a ver unos ejemplos:
Comprobemos si 2/5 y 4/10 son equivalentes.
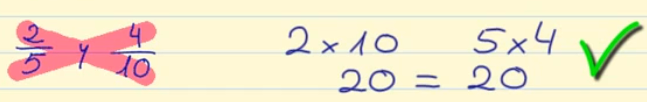
2 x 10 = 20 5 x 4 = 20
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.
Ahora vamos a comprobar si 3/7 y 7/3 son fracciones equivalentes.
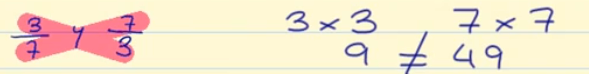
3 x 3 = 9 7 x 7 = 49
Como el resultado no es el mismo, podemos decir que 3/7 y 7/3 no son equivalentes.
¿Como podemos calcular fracciones equivalentes?
Por amplificación
Multiplicando numerador y denominador por el mismo número.
Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.
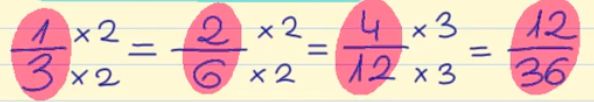
Si multiplicamos por 2: 1 x 2 = 2 3 x 2 = 6
por lo tanto la fracción 2/6 es equivalente a la fracción 1/3
Si volvemos a multiplicar por 2: 2 x 2 = 4 6 x 2 = 12
por lo tanto la fracción 4/12 es equivalente a 1/3 y a 2/6
Si ahora multiplicamos por 3: 4 x 3 = 12 12 x 3 = 36
por lo tanto 12/36 es una fracción equivalente a 1/3, a 2/6, y a 4/12
Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.
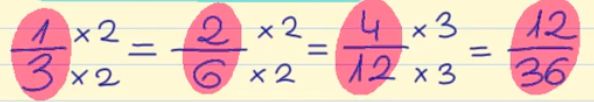
Si multiplicamos por 2: 1 x 2 = 2 3 x 2 = 6
por lo tanto la fracción 2/6 es equivalente a la fracción 1/3
Si volvemos a multiplicar por 2: 2 x 2 = 4 6 x 2 = 12
por lo tanto la fracción 4/12 es equivalente a 1/3 y a 2/6
Si ahora multiplicamos por 3: 4 x 3 = 12 12 x 3 = 36
por lo tanto 12/36 es una fracción equivalente a 1/3, a 2/6, y a 4/12
Por simplificación
Dividiendo numerador y denominador por un divisor común de ambos.

Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.
12 : 2 = 6 30 : 2 = 15
por lo tanto 6/15 es una fracción equivalente a 12/30
Ahora podemos dividirlos entre 3.
6 : 3 = 2 15 : 3 = 5
por tanto las fracciones 2/5, 6/15 y 12/30 son equivalentes.
ACTIVIDAD: Realizar los siguientes ejercicios, en el cuaderno del curso.
Clasificar las siguientes fracciones en propias e impropias.
b) Realizar los siguientes ejercicios

Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.
12 : 2 = 6 30 : 2 = 15
por lo tanto 6/15 es una fracción equivalente a 12/30
Ahora podemos dividirlos entre 3.
6 : 3 = 2 15 : 3 = 5
por tanto las fracciones 2/5, 6/15 y 12/30 son equivalentes.
ACTIVIDAD: Realizar los siguientes ejercicios, en el cuaderno del curso.
Clasificar las siguientes fracciones en propias e impropias.
b) Realizar los siguientes ejercicios
Suscribirse a:
Comentarios (Atom)








