Factorizar en números primos

¿Qué es factorizar?

Factorizar es escribir un número como la multiplicación de otros números.

Por ejemplo, factorizamos el número 12.

12 = 3 x 4

12 = 2 x 6

12 = 1 x 12

Los tres casos son ejemplos de factorización.

¿Qué es un número primo?

Ahora vamos a ver lo que es un número primo: son los números que solo son divisibles entre él mismo y entre 1.

Por ejemplo, 5 es un número primos porque solo es divisible entre 5 y entre 1. Pero 6 no es un número primo, porque es divisible entre 1, 2,3 y 6.

Esta es la tabla se representa en amarillo los números primos menores que 100: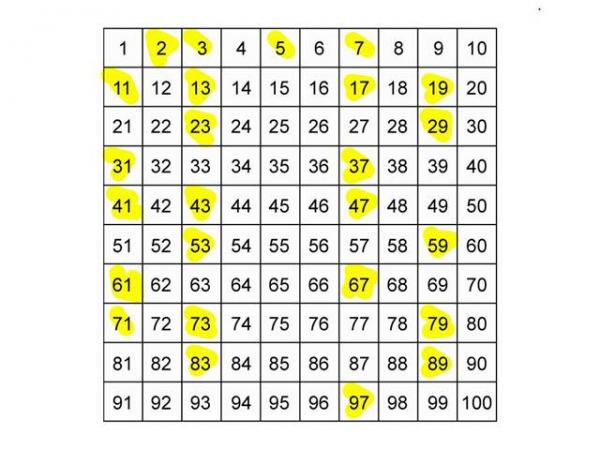

¿Qué es factorizar en números primos?

¡Exacto! Factorizar en números primos es escribir cualquier número como la multiplicación de números primos.

Vamos a verlo con un ejemplo: vamos a factorizar el 36

Elegimos un número primo  por el que sea divisible, por ejemplo el 2

 36 : 2 = 18

Ahora dividimos el 18 entre otro número primo

18 : 2 = 9

Ahora dividimos el 9

9 : 3 = 3

Y por último dividimos el 3, que como es un número primo solo podemos dividirlo entre él mismo

3 : 3 = 1

Por lo tanto, el número 36 escrito en factores primos es: 2 x 2 x 3 x 3

También podemos escribir los factores en forma de potencia, ya que el 2 se está multiplicando 2 veces y el 3 se está multiplicando dos veces: 36 = 22 x 32

Actividad; Factorizar las siguientes cantidades en el cuaderno y enviar foto.

• 54
• 76
• 52
• 49
• 56
• 50
• 45
• 26
• 27
• 33

Factorización prima

La factorización prima es el proceso de descomponer un número en sus factores primos.

Número Primo: es un número que sólo se puede dividir entre uno y entre sí mismo.

Factor: un número que puede ser dividido en otro número. Por ejemplo: 1, 2, 3, 4, 6 y 12 son factores de 12.

Ejemplos:

10 = 2 × 5, ambos factores 3 y 5 son números primos

12 = 2 × 2 × 3, ambos factores 2 y 3 son números primos

42 = 2 × 3 × 7, todos los factores 2, 3 y 7 son números primos

1 - Encuentre la factorización prima de 30.

PASO 1:

Divida el número dado por el primer número primo 2 si es divisible (si no fuera por los siguientes números primos 3, 5, 7 ... y así sucesivamente):

30 ÷ 2 = 15

PASO 2:

Divida el resultado de la división en el paso 1 por el primer número primo 2 si es posible (si no fuera por los siguientes números primos 3, 5, 7 ... y así sucesivamente):

15 ÷ 3 = 5

PASO 3: El resultado de la división en el paso 2 es el número primo 5. Nos detenemos.

La factorización de 30 implica todos los divisores y el último resultado: 30 = 2 × 3 × 5

2 - Encuentra la factorización prima de 60.

Presentamos el "método de árbol" de factorización prima que se basa en el método de división, pero su presentación es ligeramente diferente. ver abajo el ejemplo a continuación.

Actividad: Escribir en su cuaderno los conceptos claves y ejemplos que se dan en los vídeos, así como anotar las preguntas o dudas respecto al tema. 

Divisor

Un divisor es una función aritmética que divide al número natural en partes exactas, por lo tanto, al dividir el cociente debe resultar un número entero (esto quiere decir que no contenga punto decimal) y el residuo o resto de la división sea 0. Matemáticamente podemos representar el divisor del número de la siguiente manera:

n = número principal/ divisores

Donde n es cualquier número natural.

Matemáticamente, la representación para identificar los múltiplos de un número es mediante la letra “D” en mayúscula y enseguida entre paréntesis el número principal del cual queremos obtener los números que sean divisores de éste, igualamos a los divisores que se encuentran encerrados en llaves de la siguiente manera:

D(número principal)= {Divisores}

Por ejemplo, los divisores de 8 se representan de la siguiente manera:

D(8) = {1, 2, 4, 8}

Los divisores de 8 se obtienen al realizar las operaciones 8/1 = 8, 8/2 = 4, 8/4 =2 y 8/8 = 1.

---

¿Cómo saber si un número es divisor?

Para saber si un número es divisor del número principal, la mejor forma es realizando la división y verificar que el cociente sea un número entero, eso quiere decir que el resto o residuo de dividir el “número principal / el número a conocer” debe ser igual a cero.

n = número principal / número a conocer

Donde n es cualquier número natural.

---

Propiedades y características de los divisores

• Todo divisor de un número principal siempre será menor que él.
• El número 1 es divisor de todos los números que sean mayores a 0.
• Todo número principal será divisor de sí mismo, dando como cociente el 1.
• Todo número primo solo es divisible por uno y de sí mismo.
• 
  

TAREA: Copiar lo mas relevante y mínimo 3 ejemplos y encontrar los divisores de 4, 14, 27, 35, 50, 54 en el cuaderno. 

Múltiplos

TAREA: calcular los múltiplos de 6, 15, 100, 8 y 20, en el cuaderno 

División de números enteros

La división de números enteros es se hace igual que la división de números naturales y mantiene la misma relación de signos que en la multiplicación de enteros.

Según la Regla de los signos, el cociente de dos números enteros es:

• Positivo: si dividiendo y divisor tienen el mismo signo.
• Negativo: si dividendo y divisor tienen diferente signo.

Ejemplos:
(+40) : (+5) = +8

(-20) : (-2) = +10

(+100) : (-25) = -4

(-80) : (+2) = -40

Tarea: resolver los siguientes ejercicios en su cuaderno, enviarme foto

a) 10 : (-5) = 

b) (-10) : (+5)=

c) 27 : (+3) =

d) 70 : (-10) =

e) 30 : (-3) = 

f) (-6) : (+2) =